неравенство будет справедливо, когда
числитель и знаменатель будут одинаковых знаков,
причём, т.к. итоговое неравенство нестрогое (≥) и знаменатель не должен быть нулю,, то в итоге получим две ситуации:
Числитель ≥0, знаменатель >0
Числитель ≤0, знаменатель <0, <br>что и отразится в системе неравенств

0} \atop {y - {x}^{2} + 2 \leqslant 0 \: \: and \: y + x< 0}} \right. \\ \\ \left \{ {{y \geqslant {x}^{2} - 2 \: \: and \: y > - x } \atop {y \leqslant {x }^{2} - 2 \: \: and \: y < - x}} \right." alt="\left \{ {{y - {x}^{2} + 2\geqslant 0\: \: and \: \: y + x > 0} \atop {y - {x}^{2} + 2 \leqslant 0 \: \: and \: y + x< 0}} \right. \\ \\ \left \{ {{y \geqslant {x}^{2} - 2 \: \: and \: y > - x } \atop {y \leqslant {x }^{2} - 2 \: \: and \: y < - x}} \right." align="absmiddle" class="latex-formula">
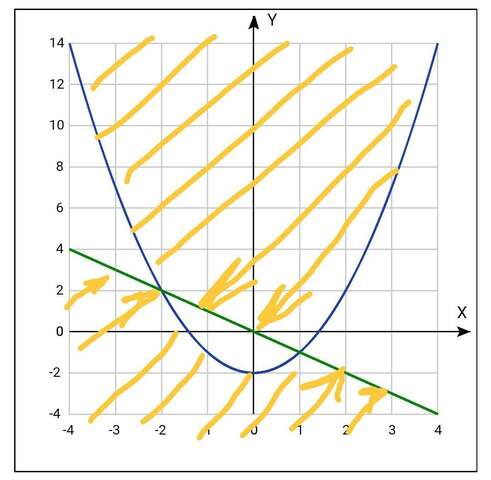
ну а дальше строим графики
у= x²-2
y= - x
и ищем области в соответствии с системой
(см выше)
Искомые обламти заштрихованы жёлтым цветом
Следует отметить, что точки графика
у= x²-2 входят в искомую область,
а точки
у=-x не входят
( чтобы избежать деления на ноль)