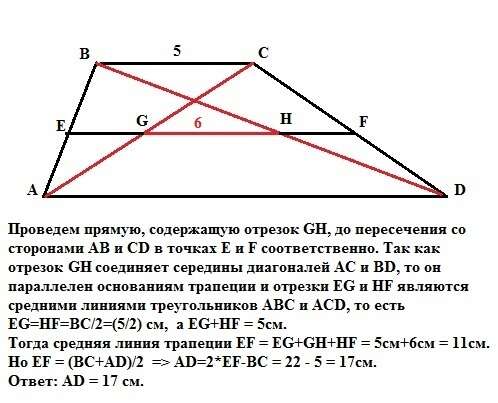
Проведем прямую, содержащую отрезок GН, до пересечения со сторонами АВ и CD в точках E и F соответственно. Так как отрезок GH соединяет середины диагоналей АС и BD, то он параллелен основаниям трапеции и отрезки EG и HF являются средними линиями треугольников АВС и АСD, то есть EG=HF=BC/2=(5/2) см, а EG+HF = 5см.
Тогда средняя линия трапеции EF = EG+GH+HF = 5см+6см = 11см.
Но EF = (ВС+AD)/2 => AD=2*EF-BC = 22 - 5 = 17см.
Ответ: AD = 17 см.