Медиана, проведенная из вершины a и b треугольника abc, друг другу перпендикулярны....

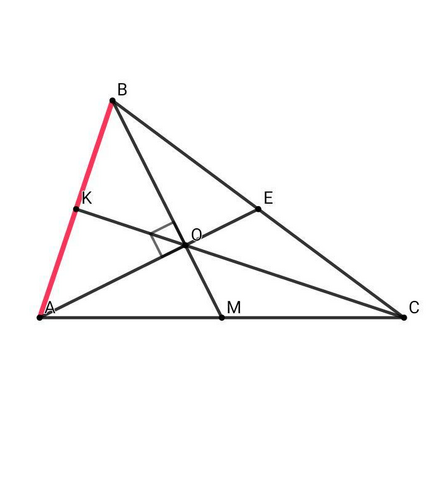
АЕ⊥ВМ, АЕ, ВМ - медианы ⇒ СК - медиана, АК = КВ. В прям-ом ΔАОВ: ОК - медиана ⇒ АК = КВ = ОК. Медианы треугольника пересекаются и точкой пересечения делятся в отношении 2 : 1, считая от вершины ⇒ ОС = 2•ОК. Значит, CK = OK + OC = (AB/2) + AB = 3AB/2 = 1,5•AB

Как известно, медиана треугольника вычисляется по формуле:

$m_{c}=\frac{1}{2}*\sqrt{2a^{2}+2b^{2}-c^{2}}\\\\$

CK² = (1/4)•(2AC² + 2BC² - AB²)

(1,5•AB)² = (1/4)•(2•34² + 2•22² - AB²)

2,25•AB² = 578 + 242 - 0,25•AB² ⇔ 2,5•AB² = 820 ⇔ AB² = 328

Ответ: 328