1. Круг вписан в круговой сектор с углом 2α. Найти отношение площади круга к площади...

Question

1. Круг вписан в круговой сектор с углом 2α. Найти отношение площади круга к площади сектора. 2. В окружность радиуса R вписан четырёхугольник ABCD, диагональ которого AC является диаметром окружности. Найти площадь треугольника ABC, если угол BAC равен α, а угол CAD равен β. Вторую задачу необязательно, но буду признательна, если поможете)

Answer 1

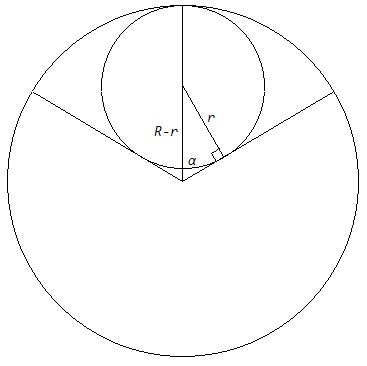
1) Окружности касаются внутренним образом, расстояние между центрами равно R-r. Окружность вписана в угол, ее центр лежит на биссектрисе, угол между линией центров и стороной равен a.

(R-r)/r= 1/sina <=> R/r= 1/sina +1 <=> r/R= sina/(sina+1)

Sк/Sс= пr^2 : пR^2*2a/360 = (r/R)^2 *180/a = (sina/(sina+1))^2 *180/a

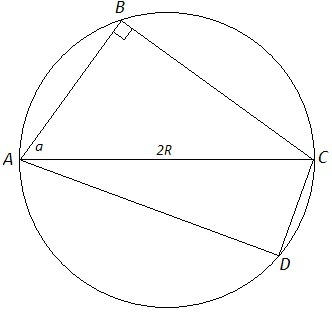
2) AB=2R*cosa, BC=2R*sina

S=AB*BC/2 =R^2*2sina*cosa =R^2*sin(2a)

Или

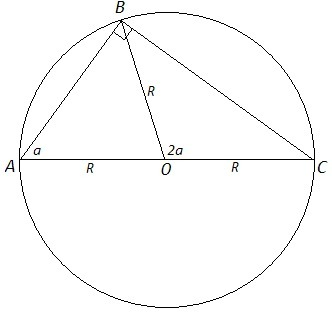
Центральный угол вдвое больше вписанного, опирающегося на ту же дугу, ∠BOC=2∠BAC=2a.

S(BOC)= R^2*sin(2a)/2

Медиана делит треугольник пополам.

S(ABC)=2S(BOC) =R^2sin(2a)

---

---

---