Помогите, пожалуйста, с комплексным числами.

Question

Дан 1 ответ

Правильный ответ

Рассмотрим комплексное число:

$z=\sqrt{3}-i\sqrt{3}$

Найдем его модуль и аргумент:

$|z|=\sqrt{(\sqrt{3})^2+(\sqrt{3})^2}=\sqrt{6}$

$\arg z=\mathrm{arctg}\dfrac{-\sqrt{3}}{\sqrt{3}}=\mathrm{arctg}(-1)=-\dfrac{\pi }{4}$

Запишем число в тригонометрической форме:

$z=\sqrt{6}\left(\cos\left(-\dfrac{\pi }{4} \right)+i\sin\left(-\dfrac{\pi }{4} \right)\right)$

Найдем значения кубического корня:

$\sqrt[3]{\rho(\cos \phi+i\sin \phi)} =\left\{\sqrt[3]{\rho}\left(\cos\dfrac{\phi+2\pi k}{3} +i\sin\dfrac{\phi+2\pi k}{3} \right)|k=0;1;2\right\}$

$(\sqrt[3]{z})_1=\sqrt[3]{\sqrt{6}}\left(\cos\dfrac{-\frac{\pi }{4}}{3} +i\sin\dfrac{-\frac{\pi }{4}}{3} \right)=\sqrt[6]{6}\left(\cos\left(-\dfrac{\pi }{12}\right)+i\sin\left(-\dfrac{\pi }{12}\right)\right)$

$(\sqrt[3]{z})_2=\sqrt[3]{\sqrt{6}}\left(\cos\dfrac{-\frac{\pi }{4}+2\pi }{3} +i\sin\dfrac{-\frac{\pi }{4}+2\pi }{3} \right)=\\=\sqrt[6]{6}\left(\cos\dfrac{\frac{7\pi }{4} }{3} +i\sin\dfrac{\frac{7\pi }{4} }{3} \right)=\sqrt[6]{6}\left(\cos\dfrac{7\pi }{12}+i\sin\dfrac{7\pi }{12}\right)$

$(\sqrt[3]{z})_3=\sqrt[3]{\sqrt{6}}\left(\cos\dfrac{-\frac{\pi }{4}+4\pi }{3} +i\sin\dfrac{-\frac{\pi }{4}+4\pi }{3} \right)=\\=\sqrt[6]{6}\left(\cos\dfrac{\frac{15\pi }{4} }{3} +i\sin\dfrac{\frac{15\pi }{4} }{3} \right)=\sqrt[6]{6}\left(\cos\dfrac{15\pi }{12}+i\sin\dfrac{15\pi }{12}\right)=\\=\sqrt[6]{6}\left(\cos\dfrac{5\pi }{4}+i\sin\dfrac{5\pi }{3}\right)=\sqrt[6]{6}\left(\cos\left(-\dfrac{3\pi }{4}\right)+i\sin\left(-\dfrac{3\pi }{4}\right)\right)$

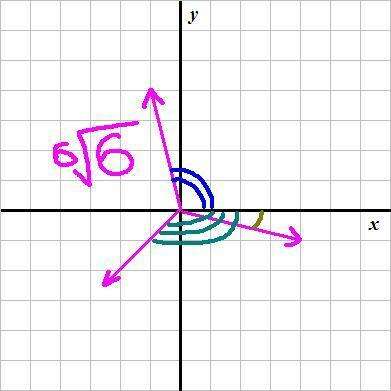
При изображении получившийся модуль числа $\sqrt[6]{6}$ является длиной векторов, а получившиеся аргументы -п/12, 7п/12, -3п/4 - углами, на которые нужно повернуть ось х для ее совмещения с направлением векторов

Artem112_zn (270k баллов) 18 Май, 20