Дана функция y=-x^2-4x-4 a)Исследуйте функцию на монотонность,если x меньше или равен -2...

Найдем производную функции и ее нули:

$y'=-2x-4;\\y'=0: x=-2.$

При x<=-2 y'>=0, то есть функция возрастает на этом промежутке.

Тогда очевидно, что наибольшее значение на отрезке [-4.5; -3.1] функция принимает в точке x=-3.1, а наименьшее - в точке x=-4.5.

$y(-4.5)=-4.5^2 + 4*4.5 - 4 = -6.25;\\y(-3.1)=-3.1^2 + 4*3.1 - 4 = -1.21.$

Ответ: а) возрастает; б) наибольшее - -1.21, наименьшее - -6.25.

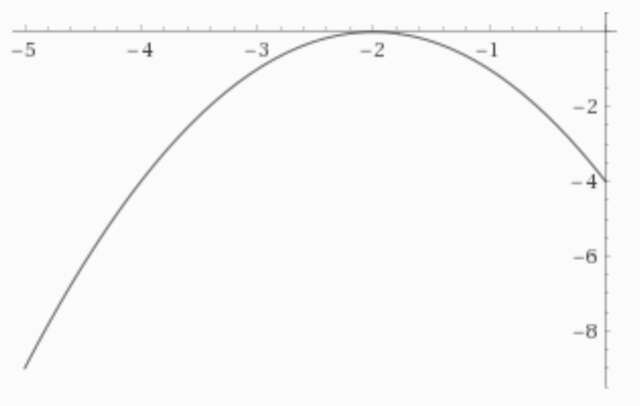
График функции на отрезке [-5; 0] для наглядности:

Дана функция y=-x^2-4x-4 a)Исследуйте функцию ** монотонность,если x меньше или равен -2...