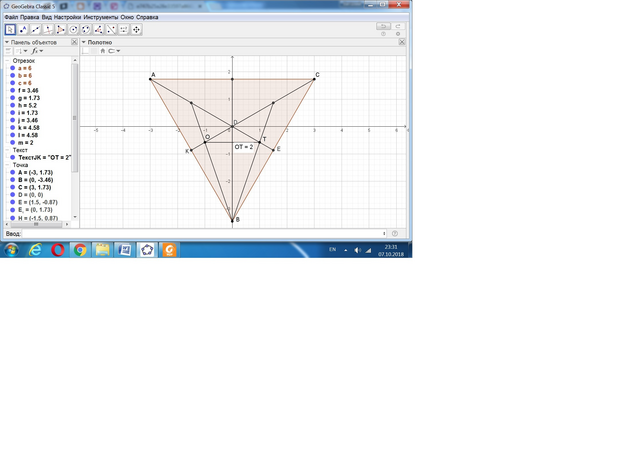
Вар 5.1. Рассмотрим горизонтальную проекцию заданного тетраэдра.
Искомый отрезок ОТ проецируется в натуральную величину, так как он параллелен основанию.
Проекции апофем ДК и ДЕ равны (1/3) высоты основания h по свойству пересечения медиан.
Отрезки в плане КО и ТЕ по этому же свойству равны (1/3) ДК или (1/9)h.
h = a*cos 30° = 6*(√3/2) = 3√3 см.
Тогда КО и ТЕ равны (3√3)/9 = √3/3 см.
Теперь рассмотрим трапецию КОТЕ. КЕ равно половине стороны, то есть 3 см.
Отрезок КО = 3 - 2*(√3/3)*cos 30° = 3 - 2*(√3/3)*(√3/2) = 3 - 1 = 2 см.