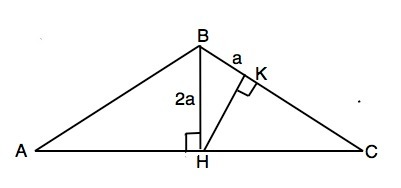
Назовём треугольник АВС, АВ=ВС; ВН - высота, медиана и биссектриса, поэтому АН=СН. НК - высота к ВС, ВК - проекция ВН на ВС. Примем ВК=а, тогда ВН=2а.
В прямоугольном ∆ ВКН катет ВК равен половине гипотенузы ВН ⇒ ∠ВНК=30°(свойство). Тогда угол НВК=60°, а НС=ВН•tg60°=2a√3.
S(ABC)=0,5•ВН•АС=ВН•СН ⇒ 2a•2a√3=√3 ⇒ 4a²=1. ⇒ a=√(1/4)=1/2. Отсюда ВН=2•1/2=1 (ед. длины).