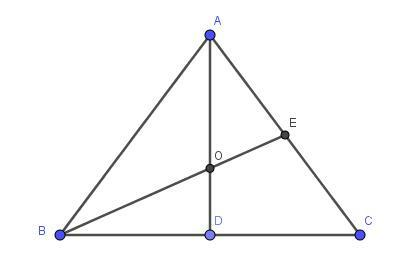
Высота AD, проведенная к основанию BC является биссектрисой и медианой. О - точка пересечения медиан. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, начиная от вершины.
Пусть AO = 2x и OD = x, тогда из условия AO = 8, решим уравнение
2x = 8
x = 4
Тогда OD = 4, следовательно, AD = AO + OD = 8 + 4 = 12
Ответ: 12