0 \\ \frac{ {x}^{2} + 10x + 25 + 25}{ ({x} - 8)(x + 6)} > 0 \\ \\ \frac{(x + 5) ^{2} + 25}{(x - 8)(x + 6)} > 0 \\ " alt=" \frac{ {x}^{2} + 10x + 50 }{ {x}^{2} - 2x - 48} > 0 \\ \frac{ {x}^{2} + 10x + 25 + 25}{ ({x} - 8)(x + 6)} > 0 \\ \\ \frac{(x + 5) ^{2} + 25}{(x - 8)(x + 6)} > 0 \\ " align="absmiddle" class="latex-formula">
так как

0" alt="(x + 5) ^{2} + 5 > 0" align="absmiddle" class="latex-formula">
то данное неравенство эквивалентно
следующему

0 \\ " alt="(x - 8)(x + 6) > 0 \\ " align="absmiddle" class="latex-formula">
решим его
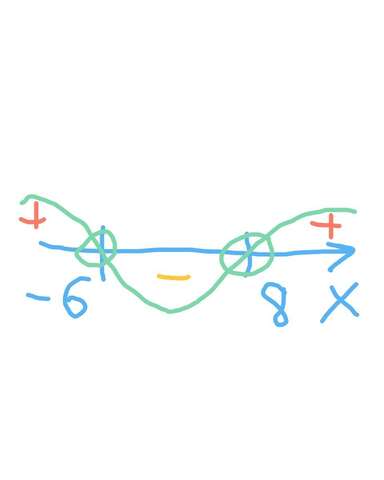
методом интервалов
(см рис)
его решением будет
х€(-∞; -6)v(8;+∞)
эти же х будут и решением исходного неравенства
Ответ:
x€(-∞; -6)v(8;+∞)