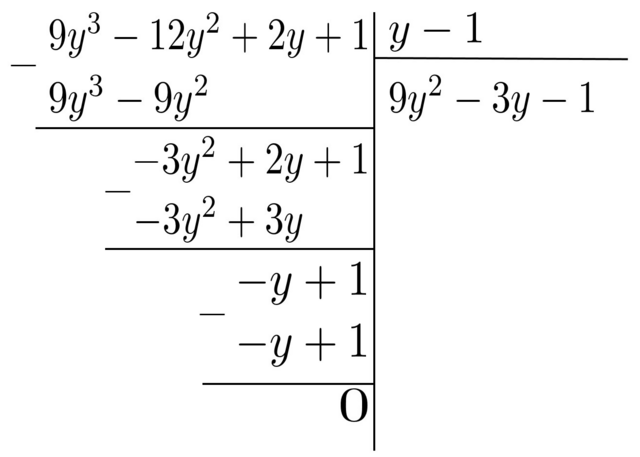Не знаю чем не понравился способ подстановки, всё нормально работает. Конечно, может есть метод и попроще, но и этот нормален.

Здесь, если кубическое уравнение имеет целые корни, то все они - делители свободного члена. В нашем случае либо  , либо
, либо  . Проверкой находим
. Проверкой находим  . Далее столбиком делим кубическое уравнение на линейное. (см. приложение)
. Далее столбиком делим кубическое уравнение на линейное. (см. приложение)



Далее, позволю себе заявить, что  , поскольку находим решения симметрических многочленов (если не веришь, можешь посчитать
, поскольку находим решения симметрических многочленов (если не веришь, можешь посчитать  руками).
руками).
Ответ.