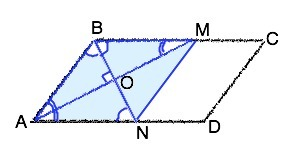
ВС|║АD, АВ - секущая. ⇒ сумма внутренних односторонних углов равна 180°. Биссектрисы делят углы пополам.⇒ из суммы углов треугольника угол ВОА=180°- 0,5•(∠АВС+∠ BAD)=90°,
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник ( для доказательства рассмотри накрестлежащие углы при секущих ВN и АМ) ⇒ ВМ=АВ, АN=AB ⇒ ВМ=АN. В ∆ ВМN отрезок ВО=ОN (т.к.в ∆ АВМ АО - медиана),⇒ МО - медиана и высота ( угол ВОМ =90° как смежный углу ВОА) ⇒ треугольник ВМN – равнобедренный и МN =ВМ Противоположные стороны четырехугольника АВMN равны и параллельны ( лежат на параллельных прямых), следовательно, АВMN– параллелограмм по определению. Кроме того, этот четырехугольник - ромб, т.к. все его стороны равны, а диагонали взаимно перпендикуляры и являются биссектрисами его углов. .