Биссектриса угла B параллелограмма ABCD пересекает сторону AD в точке K, AK:KD = 3:2....

Ответ: Р=64 см

Объяснение:

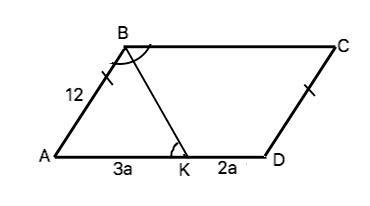
Примем коэффициент отношения АК:КD равным а. ⇒ АD=3а, КD=2a.

ВК - биссектриса ⇒ ∠СВК=∠АВК. Но ∠СВК=∠ВКА как накрестлежащие при пересечении параллельных ВС и АD секущей ВК. Поэтому ∠АВК=∠АКВ. Треугольник АВК равнобедренный по равенству углов при основании ВК. ⇒ АК=АВ=12 см.

Тогда 3а=12

а=12:3=4

АD=3а+2а=5а.

АD=5•4=20 см

CD=AB=12 см

BC=AD=20 см

P(ABCD)=2•(12+20)=64 (см)