Исследлвать функцю y=x^3/ x^2-4

ДАНО: Y = x³/(x²-4)

Провести исследование.

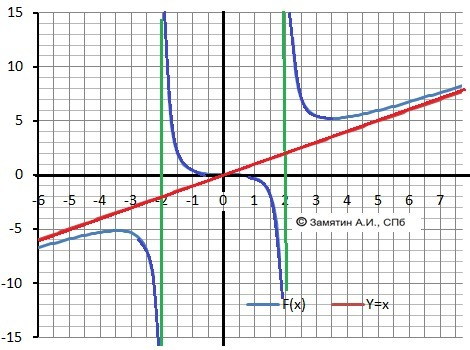
РЕШЕНИЕ - сразу рисунок с графиком в приложении в помощь расчетам.

1. Область определения. Y = x³/(x-2)*(x+2) x≠ -2 x ≠ 2.

X∈(-∞;-2)∪(-2;2)∪(2;+∞).

2. Вертикальные асимптоты: х = -2 и х = 2 - (зеленые).

3. Наклонная асимптота: y = k*x + b. Коэффициент наклона

$k= \lim_{x \to \infty}\frac{y(x)}{x}=\frac{x^2}{x^2-4}=\frac{1}{1-\frac{4}{x^2} } =1$

Наклонная асимптота: y = x - (красная).

4. Поведение на бесконечности и в точках разрыва.

Пример. $\lim_{x \to \infty} y(x) =+oo \\ \lim_{x \to \nfty2+} y(x)=+oo\\$

Остальные по графику функции - самостоятельно.

5. Проверка на чётность

y(-x) = - x³/(x²-4) = - y(x) - функция нечётная.

6. Поиск экстремумов - через корни первой производной.

$y'(x)=(\frac{x^3}{x^2-4})'=\frac{3x^2}{x^2-4}-\frac{2x^4}{(x^2-4)^2}$

Корни производной: х₁ = - 2√3, х₂= 0 , х₃ = 2√3 ≈ 3,5.

7. Минимум y(x1) = - 3√3. Максимум y(x3) = 3√3.

8. Выпуклая - Х∈(-∞;-2)∪(0;2). Вогнутая - Х∈(-2;0)∪(2;+∞)