ОДЗ (Область допустимых значений): x ≠ -4
1 способ:

 0}} \right. \\\left \{ {{x(3-x)\leq0} \atop {x+4<0}} \right." alt="\left \{ {{x(3-x)\geq0} \atop {x+4>0}} \right. \\\left \{ {{x(3-x)\leq0} \atop {x+4<0}} \right." align="absmiddle" class="latex-formula">
0}} \right. \\\left \{ {{x(3-x)\leq0} \atop {x+4<0}} \right." alt="\left \{ {{x(3-x)\geq0} \atop {x+4>0}} \right. \\\left \{ {{x(3-x)\leq0} \atop {x+4<0}} \right." align="absmiddle" class="latex-formula">
 -4}} \right. \\\left \{ {{x\in(-\infty;0]\cup[3;+\infty)} \atop {x<-4}} \right." alt="\left \{ {{x\in[0,3]} \atop {x>-4}} \right. \\\left \{ {{x\in(-\infty;0]\cup[3;+\infty)} \atop {x<-4}} \right." align="absmiddle" class="latex-formula">
-4}} \right. \\\left \{ {{x\in(-\infty;0]\cup[3;+\infty)} \atop {x<-4}} \right." alt="\left \{ {{x\in[0,3]} \atop {x>-4}} \right. \\\left \{ {{x\in(-\infty;0]\cup[3;+\infty)} \atop {x<-4}} \right." align="absmiddle" class="latex-formula">
![x\in[0,3]\\x\in(-\infty,-4) x\in[0,3]\\x\in(-\infty,-4)](https://tex.z-dn.net/?f=x%5Cin%5B0%2C3%5D%5C%5Cx%5Cin%28-%5Cinfty%2C-4%29)
Учитывая ОДЗ, окончательный ответ:
![x\in(-\infty,-4)\cup[0,3] x\in(-\infty,-4)\cup[0,3]](https://tex.z-dn.net/?f=x%5Cin%28-%5Cinfty%2C-4%29%5Ccup%5B0%2C3%5D)
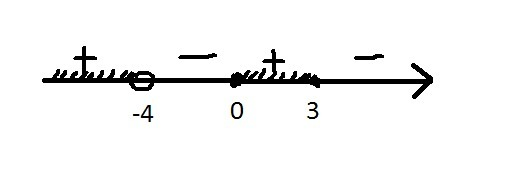
2 способ:


Дальше см. изображение
Ответ: ![x\in(-\infty,-4)\cup[0,3] x\in(-\infty,-4)\cup[0,3]](https://tex.z-dn.net/?f=x%5Cin%28-%5Cinfty%2C-4%29%5Ccup%5B0%2C3%5D)