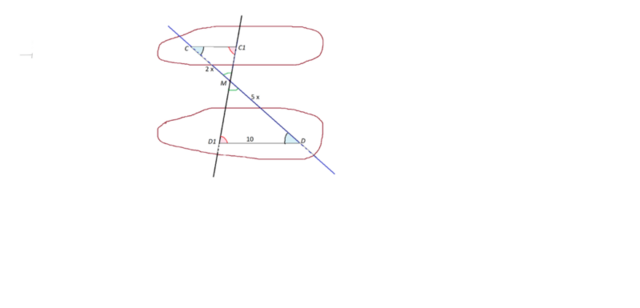
Через точку M лежащую между параллельными плоскостями α и β проведены прямые l и k.
l пересекает α и β в точке C и D, k пересекает α и β в точках C1 и D1.
Найти CC1,если DD1=10 см, а CD/CM=7/2
-------------------
Решение начнем с рисунка.
Так как плоскости
α и
β параллельны, а прямые
l и
k пересекаются вне их, отрезки
СС1 и ДД1, лежащие в параллельных плоскостях, параллельны.
Рассмотрим треугольники СМС1 и ДМД1
При точке М их углы равны ( вертикальные).
Углы ДСС1 и СДД1 равны как углы при пересечении параллельных прямых СС1 и ДД1 секущей.
Углы СС1Д1 и С1Д1Д равны на том же основании.
Треугольники СМС1 и ДМД1 подобны.
СД
:СМ=7/2
Следовательно, МД
:СМ=(СД-СМ
):СМ =(7-2)
:2=5/2
Коэффициент подобия треугольников
5/2
ДД1
:СС1=5
:2
10
:СС1=5
:2
5СС1=20
СС1=20
:5=4
Ответ
: СС1=4