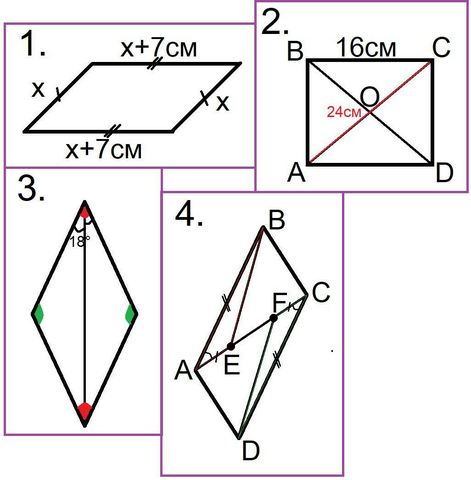
1.
В параллелограмме противоположные стороны равны.
Пусть меньшая сторона равна x, тогда противоположная равна x, а смежные с ней равны x+7см. Периметр 54см, поэтому
2·(x + x+7см) = 54см = 4x+14см
4x = 54-14 = 40см
x = 40:4 = 10см - длина каждой из двух меньших сторон.
x+7см = 10+7 = 17см - длина двух других сторон.
Ответ: 10см, 17см, 10см и 17см.
2.
В прямоугольнике противоположные стороны равны (BC=AD), диагонали тоже равны (AC=DB), а точкой пересечения делятся пополам.
AO = AC:2 = 24:2 = 12см
DO = DB:2 = AC:2 = 12см
AD = BC = 16см
 AO+DO+AD = 12+12+16 = 40см
AO+DO+AD = 12+12+16 = 40см
Ответ: 40см.
3.
Противоположны углы в ромбе равны, смежные углы дают в сумме 180°, а диагонали служат биссектрисами углов.
Сторона образует с диагональю угол в 18°, это же диагональ проходит через углы в 18°·2=36° т.к. она делит их пополам.
Остальные два углы равны между собой и вместе с углом в 36° дают 180°. То есть они равны 180°-36° = 144°.
Ответ: 144°, 36°, 144° и 36°.
4.
ΔAEB = ΔCFD по двум сторонам и углу между ними (AB=CD как противоположные стороны параллелограмма; ∠BAE=∠DCF как накрест лежащие; AE=CF по условию).
BE = DF, как стороны лежащие напротив равных углов (∠BAE=∠DCF), в равных треугольниках. Доказано.