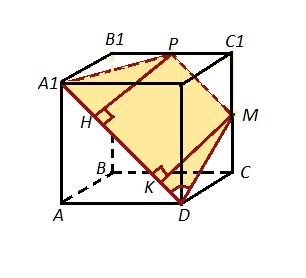
Достроим сечение, проходящее через прямые А1Д и ДМ. Это будет трапеция А1ДМР, МР║А1Д , МР=0,5*В1С=0,5*А1Д (А1Д=В1С) .
А1Д=√(АА1²+АД²)=√(1+1)=√2 , МР=0,5*√2=√2/2 .
Проведём высоты трапеции: РН⊥А1Д и МК⊥А1Д .
КД=0,5*(А1Д-НК)=0,5*(А1Д-РМ)=0,5*(√2-√2/2)=0,5*(√2/2)=√2/4 .
ΔКДМ: ∠ДКМ=90° , МД=√(СД²+МС²)=√(1²+0,5²)=√(1+1/4)=√(5/4)=√5/2 ,
cos∠КДМ=КД/МД=√2/4:√5/2=√2/(2·√5)=1√10 .
∠КДМ=arccos(1/√10)=arccos(√10/10) .