Вычислите площадь фигуры, ограниченной линиями y=x^2-4x+5 и у=5

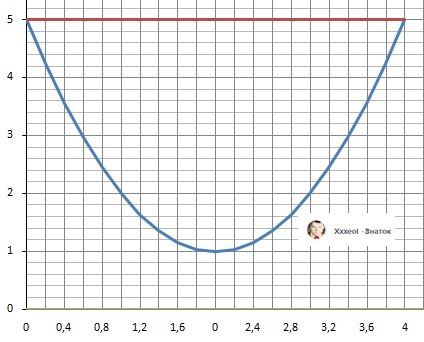
Рисунок к задаче в помощь к расчету.

ДАНО: y(x) = x² - 4x + 5 и f(x) = 5 - переобозначили для записи уравнений

НАЙТИ: S(x) = ? - площадь фигуры.

РЕШЕНИЕ

Площадь фигуры - интеграл (первообразная) разности функций.

1. Находим разность функций - !!! -прямая выше параболы !!!

1) s(x) = f(x) - y(x) = x² - 4x = x*(x - 4) = 0

Находим пределы интегрирования - решение ур. 1) a = 4, b = 0.

2) Находим первообразную функцию - интегрируем.

$S(x)=\int\limits^4_0 ({-4x+x^2}) \, dx=-4 \frac{x^2}{2}+ \frac{x^3}{3}$

(мне нравится такая запись - в порядке увеличения степени и запись дробью)

Вычисляем разность на пределах интегрирования.

S(4)= 32 - 21 1/3 = 10 2/3, S(0) = 0

S = S(4) - S(0) = 10 2/3 - площадь - ОТВЕТ (10,667)