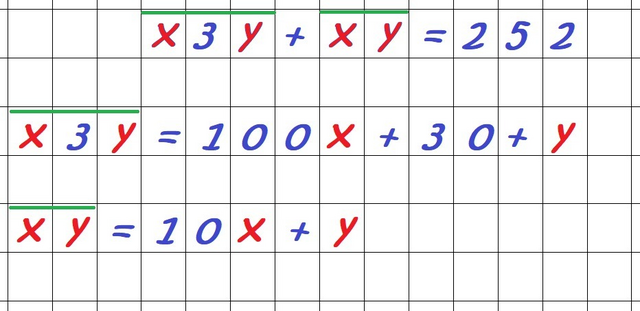
У нас есть два числа. Первое число трёхзначное, а второе - двухзначное, т. к. оно получено удалением одной цифры из первого числа.
Разложим эти числа поразрядно, попутно вводя переменные:
(100x + 30 + y) - первое число, (10x + y) - второе число.
Причём x и y - какие-то цифры от 0 до 9.
Процесс разложения можно посмотреть в приложении.
Черта над числами "x3y" и "xy" означает, что это не произведение, а одно число.
Сумма двух чисел даст нам 252, запишем это в виде уравнения:
(100x + 30 + y) + (10x + y) = 252;
100x + 30 + y + 10x + y = 252;
110x + 2y + 30 = 252.
Учитывая, что y - число от 0 до 9, очевидно y = 1.
Тогда получаем:
110x + 2 + 30 = 252;
110x = 252 - 32;
110x = 220;
x = 2.
Таким образом, получаем, что x = 2, y = 1.
Значит, искомые числа: 231 и 21.
Ответ: 231 и 21.
Вообще говоря, решить задачу можно и проще.
Смотрим на первую строку приложения. Получаем:
Из разряда единиц: y + y = 2, значит y = 1.
Из разряда десятков: 3 + x = 5, тогда x = 2.
Но это "устный" путь. Для записи в тетрадь лучше использовать выше описанный способ.