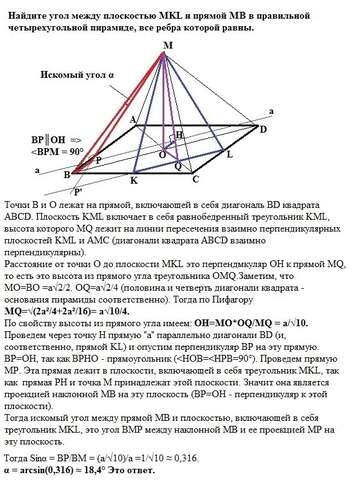
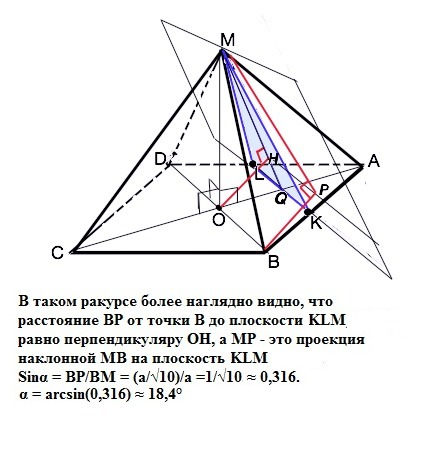
Искомый угол - <ВМP. ВP=OH - расстояние от прямой BD до плоскости MKL (высота из прямого угла MOQ). Тогда PM - проекция BM на плоскость MKL. МO=BO = a√2/2. OQ=a√2/4. MQ=√(2a²/4+2a²/16) = a√10/4. ОН=BP=MO*OQ/MQ = a/√10.</p>
Sinα = BP/BM = (a/√10)/a = 1/√10
Или подробнее:
Точки В и О лежат на прямой, включающей в себя диагональ BD квадрата АВСD. Плоскость KML включает в себя равнобедренный треугольник KML, высота которого МQ лежит на линии пересечения взаимно перпендикулярных плоскостей KML и AMC (диагонали квадрата АВСD взаимно перпендикулярны). Расстояние от точки О до плоскости MKL это перпендмкуляр ОН к прямой MQ, то есть это высота из прямого угла треугольника OMQ. Заметим, что треугольник МОВ - равнобедренный (BD=a√2, BO=a√2/2, а так как все ребра пирамиды равны, то в треугольнике ВОМ катет МО=a√2/2). МO=BO =a√2/2. OQ=a√2/4 (половина и четверть диагонали квадрата - основания пирамиды соответственно). Тогда по Пифагору MQ=√(2a²/4+2a²/16)= a√10/4.
По свойству высоты из прямого угла имеем: ОН=MO*OQ/MQ = a/√10.
Проведем через точку Н прямую "а" параллельно диагонали BD (и, соответственно, прямой KL) и опустим перпендикуляр ВР на эту прямую. ВР=ОН, так как ВРНО - прямоугольник (
Sinα = BP/BM = (a/√10)/a =1/√10 ≈ 0,316.
α = arcsin(0,316) ≈ 18,4° Это ответ.