1) Прямая АВ лежит в плоскостях АВС , АВD , АВF .
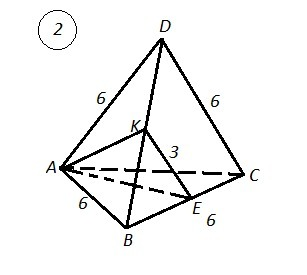
2) Так как точки К и Е - середины рёбер BD и ВC правильного тетраэдра, то BK=KD=6:2=3 , ВЕ=ЕС=6:2=3 , КЕ - средняя линия грани BCD и КЕ║DC, КЕ=6:2=3 (как средняя линия треугольника).
АК и АЕ - высоты, медианы и биссектрисы правильных треугольников АВD и BCD. Они равны √(6²-3²)=√27=3√3.
Периметр сечения АКЕ равен Р=3+2*3√3=3+6√3.