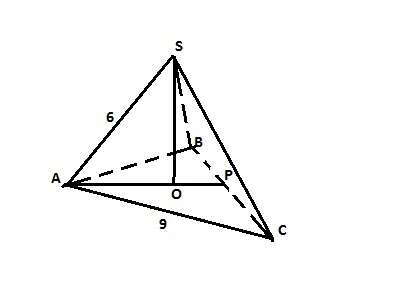
В правильной треугольной пирамиде вершина проецируется в центр основания - правильного треугольника. Этот центр делит высоту основания в отношении 2:1, считая от вершины треугольника. Высота треугольника равна (√3/2)*а, где а - сторона треугольника. В нашем случае h=(√3/2)*9. Тогда АО = (2/3)*h - это катет прямоугольного треугольника, образованного высотой пирамиды (второй катет) и ребром пирамиды (гипотенуза). АО=(√3*9/2)*(2/3) = 3√3. По Пифагору найдем высоту пирамиды: Н=√(SA²-(АО)²) или Н=√(36-27) = 3см. Это ответ.