Help пожалуйста очень надо.

Question

Дан 1 ответ

Правильный ответ

$1.~~~y = 2x^{-3}=\dfrac{2}{x^3}$

График функции - гипербола. Показатель степени - нечётный, 2>0; расположение ветвей в первой/третьей четвертях.

Область определения : x≠0 ⇒ D(y) = (-∞;0)∪(0;+∞)

x = 0; y = 0 - вертикальная и горизонтальная асимптоты.

$y(-x) = \dfrac{2}{(-x)^3}=-\dfrac{2}{x^3}=-y(x)$ - нечётная функция, центральная симметрия относительно начала координат.

Точки для построения в первой четверти :

x₁= 1; y₁= 2; x₂= 2; y₂= 1/4; x₃= 3/4; y₃= 128/27≈ 4,7; ==========================================

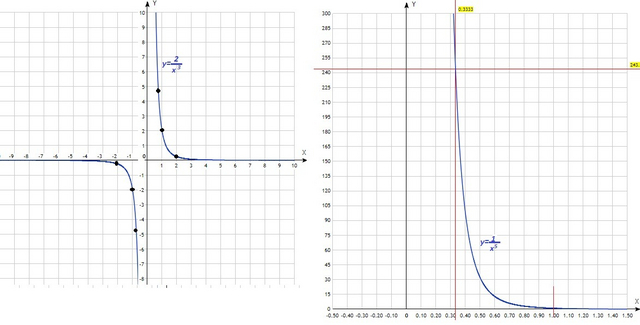
2. y = x⁻⁵ $x \in \Big[\dfrac{1}{3}; 1\Big]$

$y = x^{-5}=\dfrac{1}{x^5}$

График функции - гипербола. Показатель степени - нечётный, 1>0; расположение ветвей в первой/третьей четвертях, функция монотонно убывающая на всей области определения.

Область определения : x≠0 ⇒ D(y) = (-∞;0)∪(0;+∞)

Точка разрыва x = 0 в интервал не попадает. Значит, функция монотонно убывающая на всем промежутке $x \in \Big[\dfrac{1}{3}; 1\Big]$ , экстремумов не имеет. Тогда наибольшее и наименьшее значения функции на границах интервала.

x₁ = 1/3; y₁ = (1/3)⁻⁵ = 3⁵ = 243 - наибольшее значение функции

x₂ = 1; y₂ = 1⁻⁵ = 1 - наименьшее значение функции

xERISx_zn (41.1k баллов) 19 Май, 20