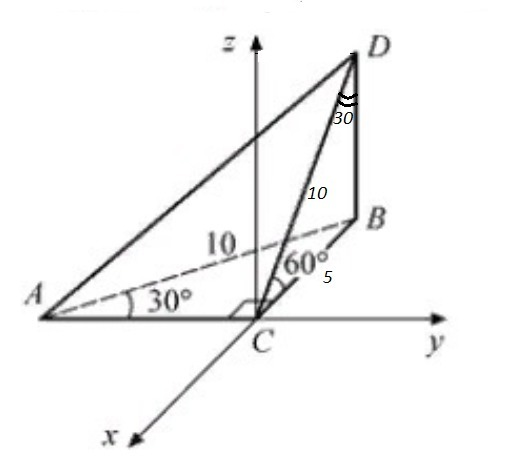
ТОчка С лежит в начале координат, значит все коордиаты этой точки равны нулю: С(0,0,0) .
Из прямоугольного ΔАВС: катет ВС лежит против угла в 30° , поэтому он равен половине гипотенузы АВ, то есть ВС=АВ:2=10:2=5 . Значит, точка В лежит на расстоянии, равном 5 , от начала координат (точки С) на оси ОХ. Но от начала координат до точки В надо двигаться вдоль оси ОХ в отрицательном направлении. Значит, точка В имеет абсциссу, равную (-5) . Точка В проектируется на ось ОУ в точку С(0,0,0) , значит ординаты у этих точек равны, то.есть ордината точки В равна 0. На ось OZ точка В проектируется в эту же точку С, значит равны и апликаты этих точек. Поэтому В(-5,0,0) .
Точка А лежит на оси ОУ на расстоянии , равном длине отрезка АС, от начала координат (точки С). Длину АС найдём из ΔАВС по теореме Пифагора: АС =√(АВ²-ВС²)=√(10²-5²)=√75=5√3. Но до точки А от начала координат надо двигаться вдоль оси ОУ в отрицательном направлении. Тогда ордината точки А равна (-5√3). На оси ОХ и OZ точка А проектируется в точку С(0,0,0). Значит , абсцисса и апликата точки А равны абсциссе и апликате точки С, и равны они 0. Итак, точка А(0,-5√3,0) .
Точка Д - вершина ΔВДС. Так как ДВ⊥ пл.(АВС)=пл.(ХОУ), то точка ∠ДВС=90° ,и точка В - проекция точки Д на пл. ХОУ. И абсцисса точки Д и её ордината будут такими же, как и у точки В(-5,0,0). Апликату точки Д найдём из прямоугольного ΔВДС. Апликата точки Д равна длине катета ВД. Т.к. ∠ДСВ=60°, то ∠ВДС=30°. Катет ВС лежит против угла в 30°, то есть ВС=СД:2 ⇒ СД=2*ВС=10 и ВД=√(СД²-ВС²)=√(10²-5²)=√75=5√3 . К точке Д от точки В надо двигаться в положительном направлении вдоль ВД, поэтому апликата точки Д равна +5√3. Итак, точка Д(-5,0,5√3) .
Замечание. Длину ВД можно найти так: ВД:BС=tg60° ⇒ ВД=BС·tg60°=5·√3 .