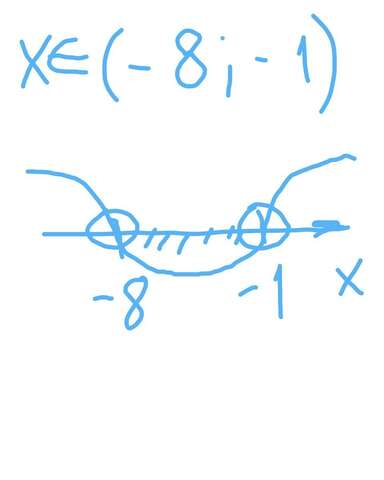2 \\ \frac{2 {x}^{2} + 18x - 4 }{ {x}^{2} + 9x + 8 } - 2 > 0 \\ \frac{2 {x}^{2} + 18x - 4 - 2 {x}^{2} - 18x - 16}{(x + 8)(x + 1)} > 0 \\ - \frac{20}{(x + 8)(x + 1)} > 0 \\ (x + 8)(x + 1) < 0" alt=" \frac{2 {x}^{2} + 18x - 4 }{ {x}^{2} + 9x + 8 } > 2 \\ \frac{2 {x}^{2} + 18x - 4 }{ {x}^{2} + 9x + 8 } - 2 > 0 \\ \frac{2 {x}^{2} + 18x - 4 - 2 {x}^{2} - 18x - 16}{(x + 8)(x + 1)} > 0 \\ - \frac{20}{(x + 8)(x + 1)} > 0 \\ (x + 8)(x + 1) < 0" align="absmiddle" class="latex-formula">
используем метод интервалов.(см рисунок)
решением неравенства будет
х€(-8;-1)