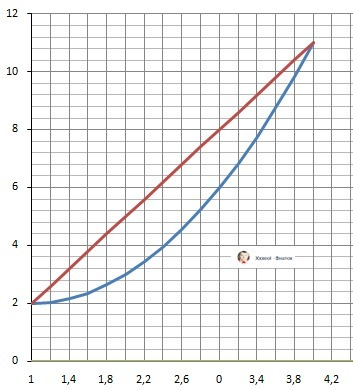
ДАНО: Y1 = x²- 2*x + 3 Y2 = 3*x - 1
НАЙТИ: S = ? - площадь фигуры.
РЕШЕНИЕ
Рисунок к задаче в приложении.
Находим разность функций и пределы интегрирования.
1) x² - 5*x + 4 = 0 - решаем
a = 4 - верхний предел и b= 1 - нижний предел.
Запишем функцию площади в другом порядке перед интегрированием:
F(x) = -4 + 5*x - x²
Находим первообразную - интеграл

Вычисляем разность функции на пределах интегрирования.
S(4) = -16+40-21 1/3 = 2 2/3
S(1) = -4 + 2.5 - 1/3 = - 1 5/6
S = S(4)-S(1) = 2.667 - 1.833 = 4.5 - площадь - ОТВЕТ