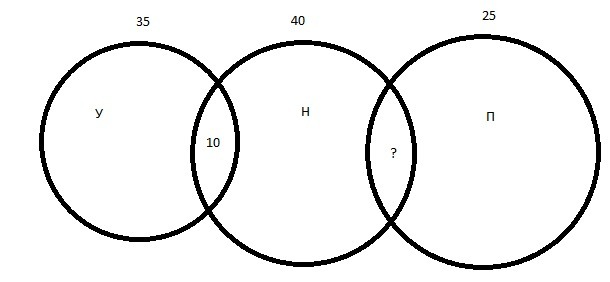
Сделал грубую диаграму Эйлера.
У - Ухо, Н - Наковальня, П -Подкова.
Пусть Н' это все запросы, содержащие Н, но не содержащие У: Н - (Н&У) = 40 - 10 = 30
Раз У и П не имеют пересечений, можем избавиться от всех запросов содержащих У: чистое и те 10, что пересекаются с Н - останется 70 - 35 = 35 запросов. Это будет (Н' | П)
Получим П' - количество запросов, содержащих П, но не содержащих Н: (Н' | П) - П = 35 - 25 = 10
Получим Н'' - количество запросов, содержащих H', но не содержащих П: (Н' | П) - Н' = 35 - 30 = 5
Значит количество запросов, содержащих Н & П = (Н' | П) - Н'' - П' = 35 - 5 - 10 = 20