Один из углов равнобедренной трапеции равен 132 градуса найдите меньший угол этой трапеции

Question

Один из углов равнобедренной трапеции равен 132 градуса найдите меньший угол этой трапеции

Answer 1

Ответ:

48°

Объяснение:

Сумма углов, прилегающих к боковой стороне трапеции, составляет 180°, поэтому если больший угол 132°, то меньший 180-132=48°.

Answer 2

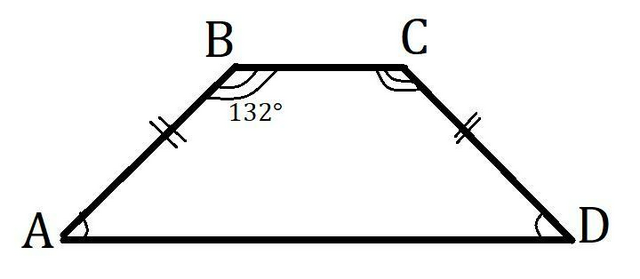
В равнобедренной трапеции углы при основаниях равны. Пусть в равнобедренной трапеции ABCD, ∠B = 132°, тогда

∠С = ∠B = 132° и ∠A = ∠D.

В выпуклом четырёхугольника сумма углов равна 360°.

∠A+∠B+∠C+∠D = 2∠A+2∠B = 360° ⇒ ∠A+∠B=180°.

∠A = 180-132 = 48°.

В трапеции углы равны: 48°, 48°, 132° и 132°.

Меньший из них - 48°.

Ответ: 48°.

---