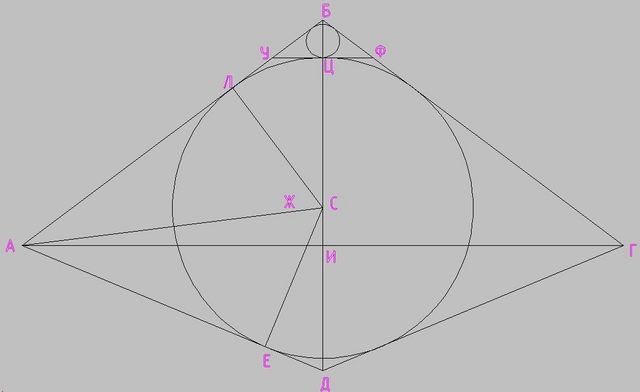
Рассмотрим осевое сечение конусов
АИ = ГИ = 12
БИ = 9
ДИ = 5
С - центр большого вписанного шара
1.
По т. Пифагора для ΔАИД
АД² = 12² + 5² = 144 + 25 = 169
АД = 13
2.
По т. Пифагора для ΔАИБ
АБ² = 12² + 9² = 144 + 81 = 225
АБ = 15
3.
Рассмотрим ΔАБД
БД = 9+5 = 14
Три стороны 13, 14, 15
полупериметр
p = 1/2(13+14+15) = 21
Его площадь по формуле Герона
S² = p(p-a)(p-b)(p-c)
S² = 21(21-13)(21-14)(21-15) = 21*8*7*6 = 7056
S = 84
4.
ΔАБД состоит из двух треугольников - ΔАБС и ΔАДС
S(АБД) = S(АБС) + S(АДС)
84 = 1/2*АБ*ЛС + 1/2*АД*ЕС
ЛС = ЕС = r - радиус большого шара
168 = 15r + 13r
168 = 28r
r = 6
5.
Рассмотрим ΔАСД
S(АСД) = 1/2*АД*СЕ = 1/2*АИ*СД
13*6 = 12*СД
СД = 13/2
СИ = СД - ДИ = 13/2 - 5 = 3/2
БЦ = БИ - ЦС - СИ = 9 - 6 - 3/2 = 3/2
6.
УФ - касательная одновременно к большому и малому шарам
ΔАБГ ~ ΔУБФ, поскольку ∠Б общий, и ∠А = ∠У, ∠Г = ∠Ф
Коэффициент подобия
k = БИ/БЦ = 9/(3/2) = 6
УФ = АГ/k = 24/6 = 4
УБ = БФ = АБ/k = 15/6 = 5/2
7.
S(УБФ) = 1/2*УФ*БЦ = 1/2*4*3/2 = 3
полупериметр ΔУБФ = 1/2*(4 + 5/2 + 5/2) = 9/2
радиус вписанной окружности ΔУБФ
S = rp
3 = r*9/2
r = 2/3
И это ответ