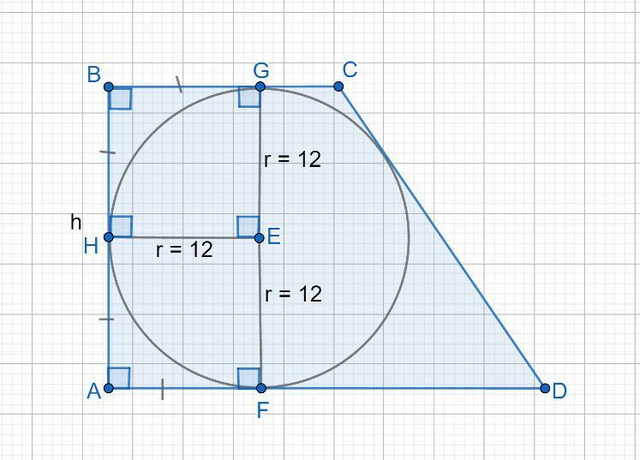
Ответ:
Высота трапеции = 24.
Пошаговое объяснение:
Дано: ABCD - прямоугольная трапеция, r = 12 (радиус вписанной окружности).
Найти высоту трапеции h.
Решение.
т.E - центр вписанной окружности.
Четырехугольник HBGE является квадратом, так как:
∠H = 90°; ∠ G =90° , угол между касательной и радиусом, проведенным в точку касания = 90°,
∠B = 90° по условию трапеция прямоугольная.
Значит ∠E = 90°, сумма углов в четырехугольнике = 360°.
⇒ HBGE прямоугольник.
В прямоугольнике противолежащие стороны равны.
GE = EH, радиусы вписанной окружности.
HB = BG, отрезки касательных проведенных из одной точки до точек касания равны.
⇒ все стороны HBGE равны между собой и равны радиусу вписанной окружности r.
Аналогично, AHEF также является квадратом, со стороной = r.
Тогда высота трапеции h = 2r = 2 * 12 = 24.