Сумма углов при большем основании трапеции 90°. докажите что расстояние между серединами...

Question

Сумма углов при большем основании трапеции 90°. докажите что расстояние между серединами оснований равно полуразности оснований

Answer 1

Пусть M и N – середины оснований BC и AD трапеции ABCD (AD > BC) и ∠A + ∠D = 90°.
Через точку M проведём прямые, параллельные AB и CD. Пусть K и L – точки их пересечения с основанием AD. Тогда ∠MKL + ∠MLK = ∠A + ∠D = 90°. Поэтому ∠KML = 90°.
Кроме того, NK = AN – AK = AN – BM = DN – CM = DN – DL = NL. Значит, MN – медиана прямоугольного треугольника KML, проведённая из вершины прямого угла. Поэтому 2MN = KL = AD – AK – LD = AD – BM – MC = AD – BC.

Answer 2

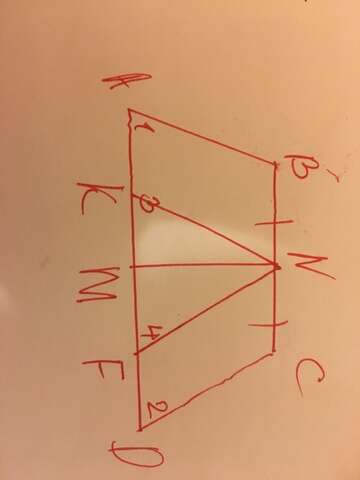
Дано:

ABCD - трапеция

∠A+∠D=90°

BN=NC

AM=MD

Доказать: MN = (AD+BC)

1) Построим NK || AB и NF || CD ABNK и NCDF параллелограммы.

2) ∠1 = ∠3 (Соответственные при AB || NK и секущей AK)

3) B ΔKNF: ∠3-∠4=90° => ∠N=90° и ΔKNF - прямоугольный, NM - медиана.

4) Следовательно, NM= KF, где KF=AD - (AK-FD) = AD - BC => MN= (AD-BC), что и требовалось доказать

---