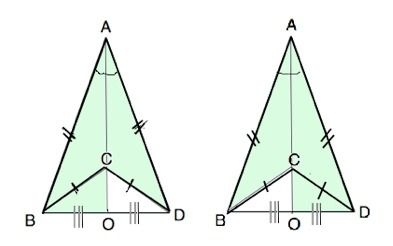
Рассмотрим треугольники ВАС и DAC. Они равны по трем сторонам - две по условию, АС - общая Следовательно, ∠ВАС=∠DAC.
В ∆ ВАD боковые стороны равны, углы при вершина А прямой АО делятся пополам ( из доказанного выше), следовательно, ∆ ВАD равнобедренный и АО его биссектриса и медиана.
∆ ВСО=∆ DCО по трем сторонам.
Периметры пятиугольников АВОСD и АВСОD –сумма равных отрезков. Следовательно, они равны.