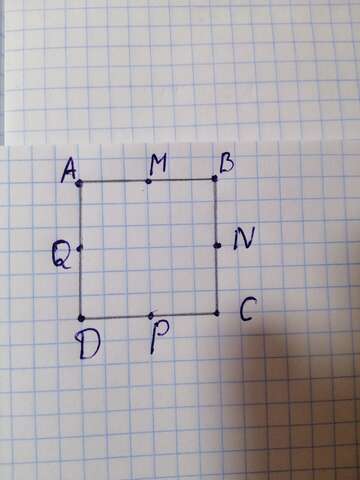
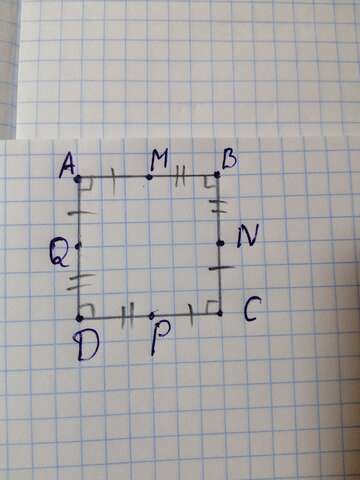1. Если чертеж понятен, рассмотри треугольники AMQ, MBN, NPC и DQP.
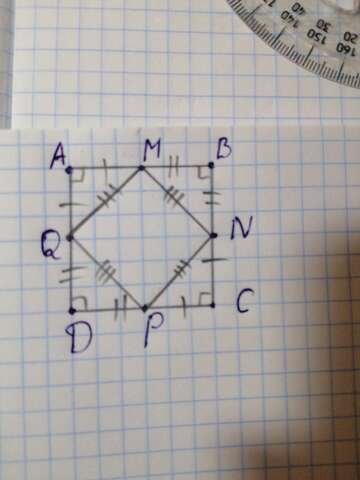
Все они прямоугольные и равны по двум катетам. Значит, гипотенузы треугольников равны.
Получили четырехугольник с равными сторонами. Значит, он ромб.
2.
Доказательство:
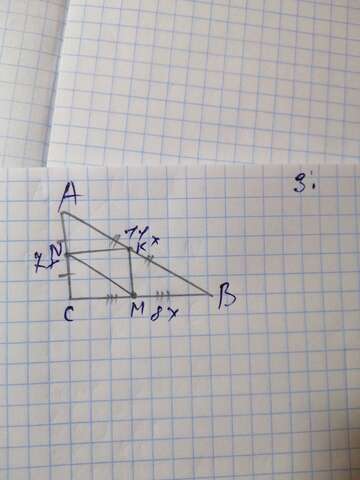
КМ и ВА - параллельные прямые, которые пересекают сторону угла С;
КМ || ВА;
АМ=МС за теоремой: параллельные прямые, которые пересекают сторону угла, отсекают от них пропорциональные отрезки. А поскольку ВК=КС (из условий задачи), то им пропорциональны отрезки АМ и МС, то есть они тоже равны: ВК/АМ=КС/МС =>(отсюда выплывает, что) АМ=МС.
3.
Решение:
Пусть коэффициент пропорциональности (k) = x. Тогда стороны треугольника равны 7х, 8х, 11х. Треугольник NKM в 2 раза меньше АСВ, то есть АСВ=104
Составляем уравнение :
104=7х+8х+11х
104=26х
Х=4
АВ=4*11=44
ВС=4*8=32
АС=4*7=28
УСЁ РЕШЕНО! *УМСТВЕННО ИЗНАСИЛОВАНА* учила то я эти темы полтора года назад... =(