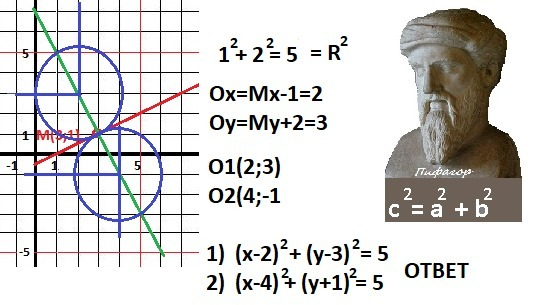ДУМАЕМ.
1. Радиус окружности равен 5.
2. От прямой из точки М надо построить перпендикуляр и найти точку на расстоянии R = √5. Таких точек будет две. Рисунок к задаче в приложении.
РЕШЕНИЕ
Уравнение окружности: (x-a)² + (y-b)² = R² = 5. (R ≈ 2.24) - надо найти координаты центра окружности - О(a,b)
1) Уравнение касательной: x - 2*y - 1 = 0 - преобразуем.
2*y = x - 1 и y = 0.5*x - 0.5 = k*x + b.
2) Уравнение перпендикуляра (радиуса)
у = - 2*х (+7 не влияет).
Отношение катетов 1 к 2. Вспоминаем теорему Пифагора.
Катеты оказались равными 1 и 2.
Находим координаты центра окружностей. Пишем уравнения окружностей.
Расчет - ОТВЕТ - на рисунке в приложении.