Произведение равно нулю тогда, когда хотя бы один из множителей равен нулю, то есть:

Это прямая, параллельная оси ординат.

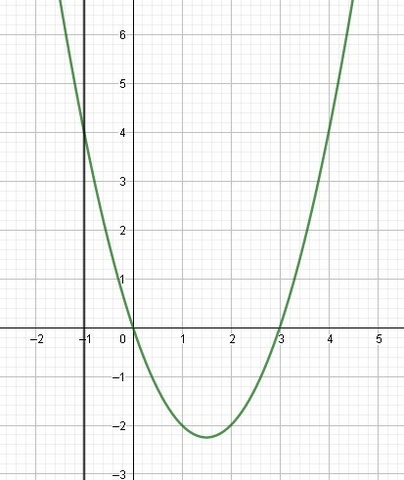
Графиком квадратичной функции является парабола, ветви которой направлены вверх, тогда


Имеем координаты вершины параболы: (1.5; -2.25).