Доказательство:
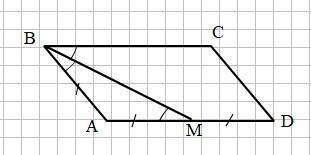
Смотри рисунок на прикреплённом фото.
ВС = 2АВ - по условию.
В параллелограмме противоположные стороны равны, то есть
АD = BC = 2АВ
АМ = 0,5AD так как М - середина стороны AD и АМ = АВ, то есть
ΔАВМ равнобедренный с основанием ВМ.
∠АВМ = ∠АМВ как углы при основании равнобедренного треугольника
∠СВМ = ∠АМВ , так как это накрест лежащие углы при ВС║ AD и секущей ВМ.
Тогда ∠СВМ = ∠АВМ и ВМ является биссектрисой ∠АВС, что и требовалось доказать.