Дан треугольник ABC и H — точка пересечения высот этого треугольника. Пусть D — середина...

Question

Дан треугольник ABC и H — точка пересечения высот этого треугольника. Пусть D — середина отрезка BC, E — середина отрезка АС. Кроме того, медианы треугольника AED пересекаются в точке H. Найдите градусную меру угла ∠ABC.

Answer 1

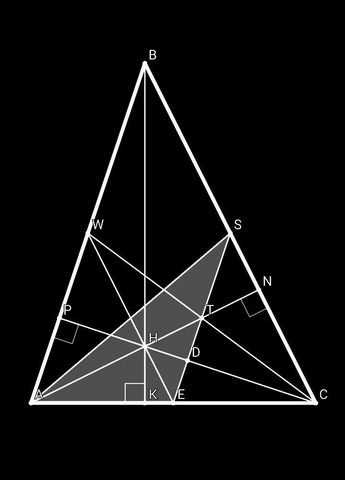
Как известно, медианы треугольника перескаются в одной точке, в отношении 2:1, считая от вершины треугольника  ⇒  AH/HT = 2/1

Применим теорему Менелая для ΔАЕТ и секущей CH:

(AH/HT)•(TD/DE)•(CE/AC) = 1  ⇔  (2/1)•(TD/DE)•(1/2) = 1  ⇔  TD = DE

В ΔCET, CD⊥SE, TD = DE  ⇒  CD - серединный перпендикуляр, SE || AB  ⇒  CP⊥AB, AP = PW, AW = WB, AN⊥WE ⇒  ΔACW - равнобедренный

точка Н - точка пересечения медиан ΔACW, AH = WH, AN⊥WE, значит, ΔAHW - прямоугольный и равнобедренный, WE || BC ⇒ ∠AWH = ∠ABC = 45°

Ответ: 45°

---