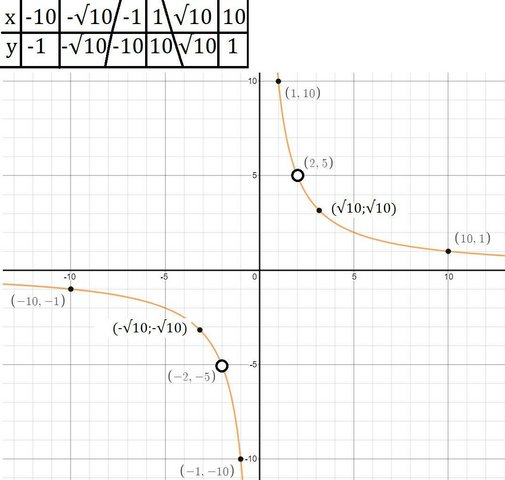
Это гипербола, асимптоты которой y=0 и x=0, график лежит в 1 и 3 четверти относительно своих асимптот, не пересекает оси координат т.к. они и являются асимптотами.
Составим таблицу из точек, чтобы определить насколько быстро функция убывает. И затем выкалим точки т.к. в этих точек исходная функция не определена.
Внизу смотри таблицу и график.