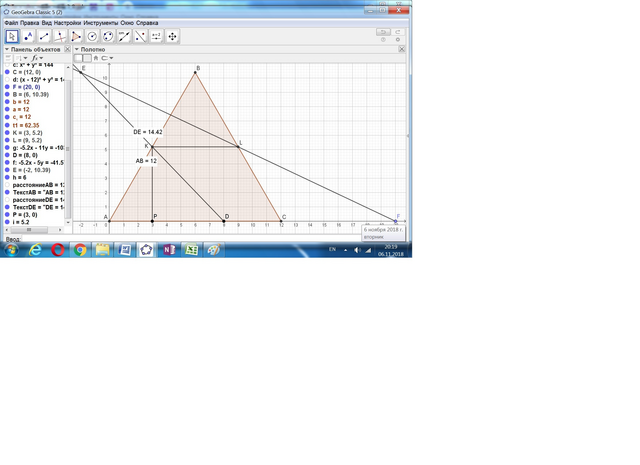
Примем длину стороны треугольника АВС за 12 единиц (для удобства кратности деления на части).
Так как отрезок KL является общей средней линией треугольников АВС и DEF, то основания их, высота и площадь одинаковы.
По заданию площадь DKLC равна 3/8 треугольника DEF, значит, и треугольника АВС. По свойству подобных треугольников АВС и KBL площадь AKLC равна (3/4) площади АВС.
Значит, площадь DKLC равна половине трапеции АKLC, которая состоит из треугольника АКD и DKLC .
Отсюда следует, что основания треугольника АКD и четырёх угольника DKLC относятся как 2 к 1.
Тогда АD = 12*(2/3) = 8.
Рассмотрим треугольник АКD. Отношение DЕ к АВ равно отношению КD к АК.
КD = √(АК² + АD² - 2*АК*АD*cos60) = √(36 + 64 - 2*6*8*(1/2)) = √52 = 2√13.
Получаем ответ: DЕ/АК = 2√13/6 = √13/3.