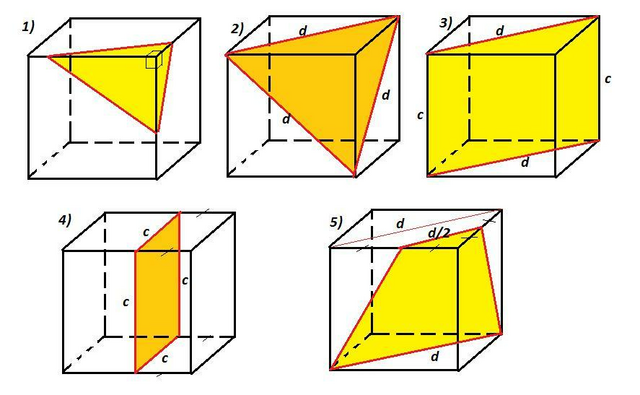
Сечением куба может быть любая из указанных в условии фигур. В приложении рисунки возможных сечений. Доказательство основывается на свойствах куба : все рёбра равны, все грани являются равными квадратами, грани попарно параллельны.
1) Произвольный треугольник получится в сечении, если от одной вершины куба отложить по трём рёбрам отрезки разного размера. Треугольник в сечении будет образован гипотенузами прямоугольных треугольников разной длины.
2) Например, правильный треугольник получится в сечении, если его сторонами будут диагонали смежных граней. Так как все грани куба равны, то диагонали граней тоже равны, то есть треугольник равносторонний.
3) Например, прямоугольник можно получить в сечении, если построить его на диагоналях противоположных граней. Двумя другими сторонами прямоугольника будут рёбра куба.
4) Например, квадрат получится в сечении, параллельном любой из граней куба.
5) Например, трапеция получится в сечении, если "наклонить" диагональное сечение. В нижней грани сечение пройдёт по диагонали, а в верхней грани по отрезку, параллельному диагонали грани.