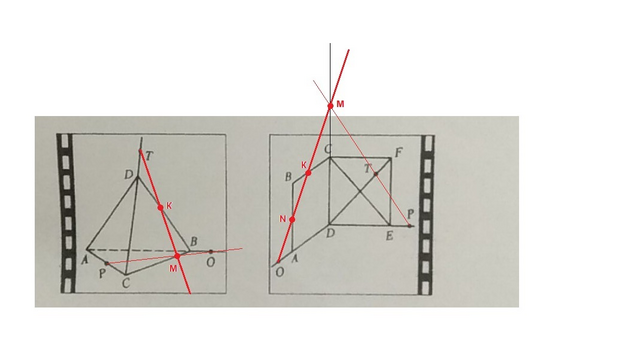
1. а) Точка Т лежит на прямой DC, значит принадлежит плоскости ADC,
точка Р лежит на прямой АС, значит принадлежит плоскости ADC.
Итак, точки Т и Р принадлежат обеим плоскостям, значит прямая ТР - линия пересечения плоскостей ТРО и ADC.
Ответ: верно.
б) Точка Т лежит на прямой DC, значит принадлежит плоскостям ТРО и DCB.
Прямая РО пересекает прямую ВС в точке М, значит точка М принадлежит плоскостям ТРО и DCB.
Значит прямая ТМ принадлежит плоскостям ТРО и DCB, т.е. является их линией пересечения.
2. а) Точки Т и Р принадлежат плоскости ТРО и плоскости CDP, значит прямая ТР - линия пересечения этих плоскостей.
б) Чтобы построить прямую, по которой пересекаются плоскости, надо найти или построить две точки, принадлежащие обеим плоскостям.
Точка О принадлежит плоскости ТРО (понятно из названия) и плоскости АВС (так как лежит на прямой AD, лежащей в этой плоскости).
Прямая ТР лежит в одной плоскости с прямой CD и пересекает ее в точке М. Прямая CD лежит в плоскости АВС, значит точка М так же принадлежит двум плоскостям.
ОМ - линия пересечения плоскостей ТРО и АВС.