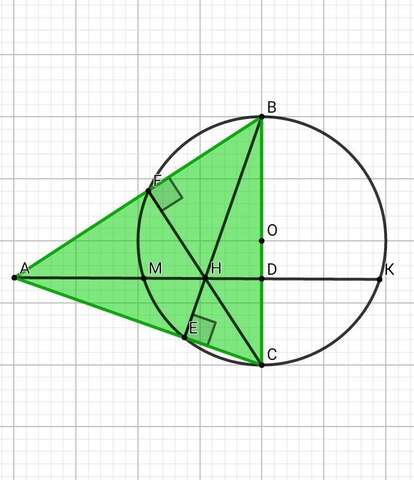
На стороне BC остроугольного треугольника ABC как на диаметре построена полуокружность, пересекающая высоту AD в точке M , AD = 16 , MD = 12 , H - точка пересечения высот треугольника ABC . Найдите AH.
РЕШЕНИЕ:
• АМ = АD - MD = 16 - 12 = 4
AK = AM + MD + DK = 4 + 12 + 12 = 28
• По свойству секущих:
АЕ • АС = АМ • АК = 4 • 28
• тр. АНЕ подобен тр. ACD по двум углам
( угол А - общий, угол АЕН = угол АDC = 90° )
Составим отношения сходственных сторон:
АЕ/AD = AH/AC = HE/CD, отсюда
АЕ/АD = AH/AC =>
AE • AC = AD • AH
AH = AE • AC / AD = 4 • 28 / 16 = 7
ОТВЕТ: 7.