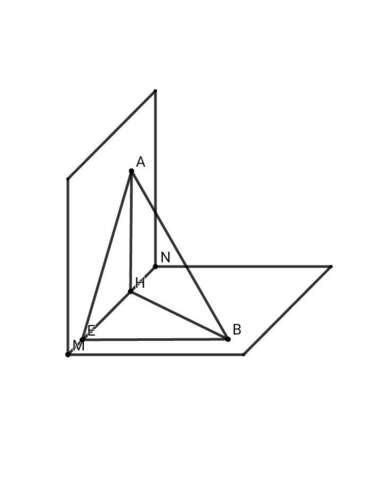
Точки А и В пренадлежит двум взаимно перпендикулярным плоскостям Альфа и Бета (А пренадлежит Альфа, В пренадлежит Бета, А не пренадлежит Бета, В не пренадлежит Альфа). Расстояние от А к прямой пересечения Альфа и Бета равно 2 см, расстояние от В к этой прямой равно 4 см. Если проекция отрезка АВ на Альфа равна 3 см, то чему равна проекция АВ на Бета?
РЕШЕНИЕ:
АН = 2 см ; ВЕ = 4 см ; АЕ = 3 см
• ВЕ перпендикулярен Альфа, соответсвенно ВЕ перпендикулярен АЕ
Отрезок АЕ - это проекция отрезка АВ на плоскость Альфа
Рассмотрим тр. АЕВ (угол АЕВ = 90°):
По теореме Пифагора:
АВ^2 = АЕ^2 + ВЕ^2 = 3^2 + 4^2 = 9 + 16 = 25
АВ = 5
• АН перпендикулярен Бета, соответсвенно АН перпендикулярен ВН
Отрезок ВН - это проекция отрезка АВ на плоскость Бета
Рассмотрим тр. АНВ (угол АНВ = 90°):
По теореме Пифагора:
АВ^2 = АН^2 + ВН^2
ВН^2 = 5^2 - 2^2 = 25 - 4 = 21
ВН = V21
ОТВЕТ: V21