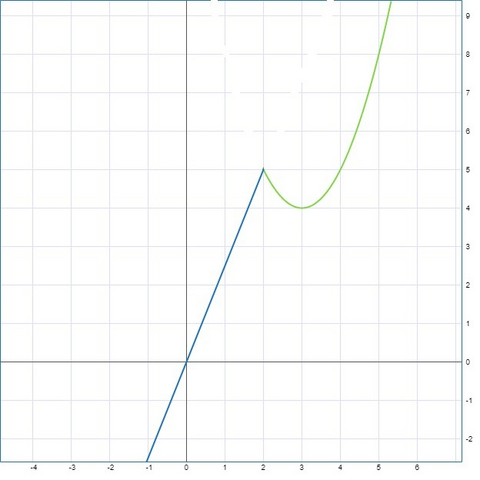
Чтобы понять, нужно построить график!
Парабола ветки вверх, и прямая, соединены вместе в эдакую загагулину на рисунке синяя и зеленные кривые.
Найдем вершину параболы: x=6/2=3; y=x²-6x+13=9-18+13=4; (3;4);
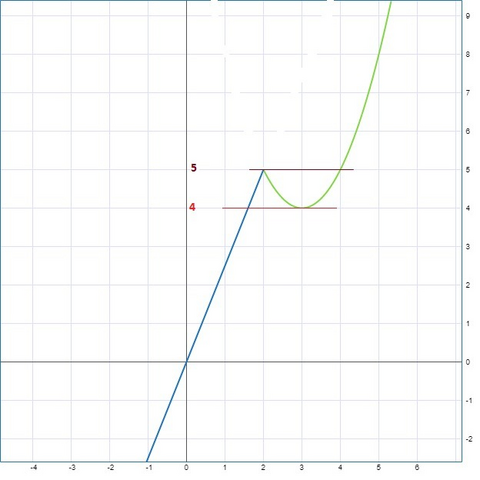
Нужно найти точки где линия параллельная ОX(y=m) пересекает нашу кривую в двух местах. y<4 и ниже у нас только одно пересечение. y=5 и выше тоже одна точка пересечения. В точках 4<t<5 - сразу три точка пересечение. И только две точки с двумя точками пересечения имеются. <strong>y=4; y=5;
Ну или m=4;5;