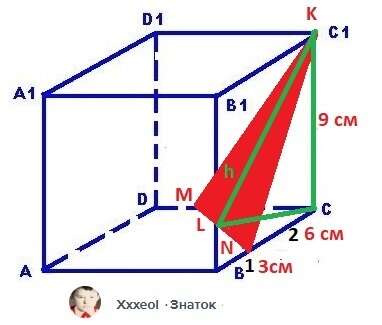
Рисунок к задаче в приложении.
НАЙТИ: S(MNK) = ? - площадь сечения.
РЕШЕНИЕ
Площадь треугольника по формуле
S = a*h/2 = MN*KL/2 - площадь.
CM = CN = 2/3 * 9 = 6 см - часть ребра куба.
MN = 6√2 - (гипотенуза ΔCMN) - основание треугольника. (например, по теореме Пифагора).
CL = 6/√2 = 3√2 - (катет ΔCLN)
И, наконец, высота KL по теореме Пифагора.
KL² = CL² + CC1² = 9*2 + 9*9 = 99
KL = √99 = 3*√11 - высота в сечении.
Осталось вычислить площадь треугольника MNK.
S(MNK) = (6√2 * 3*√11)/2 = 9*√2*√11 = 9√22 - площадь - ОТВЕТ (≈42,2)