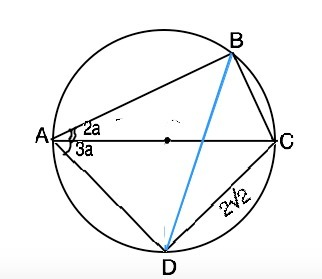
Диагональ АС четырехугольника АВСD является диаметром окружности. описанной около этого четырехугольника. Вычислить длину диагонали BD, если АС=4, CD=2√2, ∠BAC:∠CAD=2:3. В ответе укажите значение (2BD-CD)
______________________
Диаметр окружности, описанной около ∆ АDC, равен 4, сторона CD=2√2. По т.синусов СD:sinCAD=2R ⇒ 2√2:sin∠CAD=4. sin∠CAD=2√2:4=√2/2 – это синус 45°. Угол САD=45°. Угол D=90° (опирается на диаметр АС). Прямоугольный ∆ CDА равнобедренный, угол АСD=45°, AD=CD=2√2. По условию ∠BAC:∠CAD=2:3. ∠ВАС=45°•2/3=30°.⇒ ∠ВАD=75°.
В треугольнике АВD угол АВD - вписанный, опирается на ту же дугу, что угол АСD, ⇒ равен ему. ∠ BАD=ВАС+САD=45°+30°=75°
По т.синусов BD:sin∠BAD=2R=AC.
BD:sin75°=4 ⇒ BD= 4•sin75 По таблице sin75°=
⇒ BD=4•(√3+1):2√2, Домножив числитель и знаменатель этой дроби на √2, получим ВD=√2•(√3+1)
Подставим полученное значение BD в нужное выражение (2BD-CD)². [2√2•(√3+1)-2√2]²= [2√2(√3+1-1)]²=(2√6)²=24
