task/30392046
_30391586
1. Найти производные
а) y ' = ( (x²+1)/(x²-2) ) ' =|| (u/v)' =(u'*v -v'*u)/v² || =( (x²+1) '*(x²-2) - (x²-2) ' * (x²+1) )/(x²-2)² =( 2x*(x²-2) - 2x* (x²+1) )/(x²-2)² = -6x/(x²-2)²
* * * или y ' = ( (x²+1)/(x²-2) ) '= ( 1 +3/(x²-2) ) ' =1' +(3*(x²-2)⁻¹) ' =0+3*( (x²-2)⁻¹) ' =3*(-1)*(x²-2)⁻²*(x²-2)' = -3(x²-2)⁻²*2x = - 6x/(x²-2)² * * *
б) y ' = ( (1+4x)³ ) ' = 3(1+4x)²*(1+4x) ' = 3(1+4x)²*4 = 12(1+4x)².
в) y ' = ( x²sin(1-3x) ) ' = || (u*v) ' =(u'*v +v'*u || =(x²)'*sin(1-3x)+(sin(1-3x) ) ' *x²=2x*sin(1-3x)+cos(1-3x)*(1-3x) '*x² =2xsin(1-3x)+cos(1-3x)*(-3)*x² =2xsin(1-3x) - 3x²cos(1-3x).
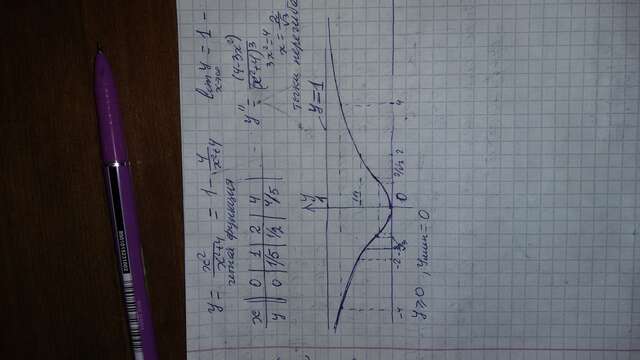
2 . Найти асимптоты функции y = x² / (x²+ 4). Построить схематично график этой функции
решение у =x² / (x²+ 4)
а) D(y): x ∈ R * * * очевидно x²+ 4 ≥ 4 ≠ 0 * * *
б) у(-x) =y(x) → четная функция ,следовательно график функции симметрично относительно оси ординат
в) (0 ; 0) ∈ Графику функции . y ≥ 0 ; min(y) =0.
г) у = x² / (x²+ 4) =1 - 4 / (x²+ 4) * * * 0 ≤ у < 1 * * * x→ ∞ ⇒ y→1 - 0
y = 1 горизонтальный асимптот см ПРИЛОЖЕНИЕ
3. Написать уравнение касательной в точке x = 1 к кривой y = 2x³+6x²+2x - 3
решение Уравнение касательной в точке x = 1: y - y(1) = y'(1)*(x-1)
y(1) =2*1³+6*1²+2*1-3 =7 ; y '=2*3x²+6*2*x+2=2(3x²+6x +1); y'(1) =20
y -7= 20(x-1) ⇔ y = 20x -13
ответ: y = 20x -13 * * * 20x -y - 13 = 0 * * *
4. Найти экстремум функции y= x³- 6x²+9x - 3
y '= (x³- 6x²+9x - 3)' = 3x²- 6*2*x+9*1+0 =3(x²-4x+3) = 3(x-1)(x-3)
+ + + + + + + (1) - - - - - - - (3) + + + + + + +
y ↑ max ↓ min ↑
y max = y(1) = 1³- 6*1²+9*1 - 3 = 1 - 6+9 - 3 = 1
y min = y(3) = 3³- 6*3²+9*3 - 3 = - 57
5. Найти наименьшее и наибольшее значения функции y= x³- 12x - 3 на отрезке [ -1 ;5]
решение y '= ( x³- 12x - 3) ' =3x²- 12 =3(x²- 4)=3(x²- 2²) = 3(x+2)(x-2)
y ' = 0 ⇔ [ x = - 2 ; x= 2 .
y(-1) = 1³- 12*1 - 3 = 1 -12 -3 = -14 ; y(5) =5³- 12*5 - 3 =125 - 60 - 3 = 62
y(-2) = (-2)³- 12*(-2) - 3 = 13 ; y(2) =2³- 12*2 - 3 = -19 .
min{ -14 ; 62 ; 13 ; -19} = -19 , max{ -14 ; 62 ; 13 ; -19} = 62
ответ: - 19 ; 62