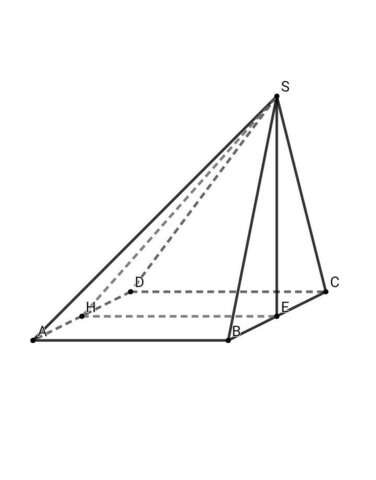
Основание пирамиды - прямоугольник, стороны которого равны 24 дм и 15 дм. Высота пирамиды проходит через середину большей стороны основания и равна 16 дм. Вычислите площадь боковой поверхности пирамиды.
РЕШЕНИЕ:
Вначале исследуем вид каждого треугольника в боковых гранях
• Рассмотрим тр. SBC:
SE - высота и медиана - по условию => тр. SBC - равнобедренный ( ВS = SC )
• SB - наклонная, SE - перпендикуляр к плоскости АВС , ВЕ - проекция наклонной SB на плоскость АВС. SE перпендикулярен ВС , ВЕ перпендикулярен АВ => по теореме о трёх перпендикулярах SB перпендикулярен АВ
Значит, тр. АВS - прямоугольный
Аналогично, тр. CDS - прямоугольный
• тр. АВS = тр. CDS по двум катетам => AS = DS . Значит, тр. ADS - равнобедренный
• В тр. ADS из вершины S на AD опустим высоту SH => AH = HD
SH перпендикулярен AD , SE перпендикулярен ЕН => по теореме о трёх перпендикулярах EH перпендикулярен AD
• Рассмотрим тр. SEH (угол SEH = 90°):
По теореме Пифагора:
SH^2 = EH^2 + SE^2
SH^2 = 15^2 + 16^2 = 225 + 256 = 481
SH = V481 дм
• Рассмотрим тр. ВES (угол BES = 90°):
По теореме Пифагора:
ВS^2 = SE^2 + BE^2
BS^2 = 16^2 + 12^2 = 256 + 144 = 400
BS = 20 дм
S бок. = S bcs + S ads + 2 • S abs = ( 1/2 ) • 24 • 16 + ( 1/2 ) • 24 • V481 + 2 • ( 1/2 ) • 15 • 20 = 192 + 12V481 + 300 = 12V481 + 492 дм^2
ОТВЕТ: 12V481 + 492 дм^2