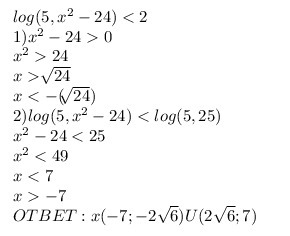0 \\x^2>24\\x>\sqrt[]{24}\\x<- (\sqrt[]{24})\\2) log(5, x^2-24)<log(5, 25)\\x^2-24<25\\x^2<49\\x<7\\x>-7\\OTBET: x(-7; -2\sqrt{6} )U(2\sqrt{6} ;7)" alt="log(5, x^2-24)<2\\1) x^2-24>0 \\x^2>24\\x>\sqrt[]{24}\\x<- (\sqrt[]{24})\\2) log(5, x^2-24)<log(5, 25)\\x^2-24<25\\x^2<49\\x<7\\x>-7\\OTBET: x(-7; -2\sqrt{6} )U(2\sqrt{6} ;7)" align="absmiddle" class="latex-formula">
